Description

Geometrically, the intuition behind Gram-Schmidt is that the difference vector, also called the error vector in least squares, between a vector and its projection onto a subspace are orthogonal to each other.

Projection

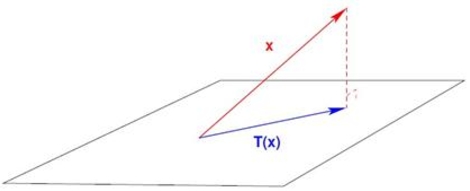
In this image, the dotted red line represents the error vector between $\vec{x}$ and its projection on the subspace. Note that the projection of $\vec{x}$ and the error vector are orthogonal to each other.

Using this property, we can then construct an orthogonal basis given a set of vectors.